1、题干
给定一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字:
- 例如,从根节点到叶节点的路径
1 -> 2 -> 3表示数字123。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
示例 1:
输入:root = [1,2,3]
输出:25
解释:
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此,数字总和 = 12 + 13 = 25示例 2:
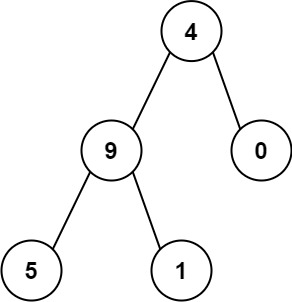
输入:root = [4,9,0,5,1]
输出:1026
解释:
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此,数字总和 = 495 + 491 + 40 = 1026
提示:
- 树中节点的数目在范围
[1, 1000]内 0 <= Node.val <= 9- 树的深度不超过
10
注意:本题与主站 129 题相同: https://leetcode-cn.com/problems/sum-root-to-leaf-numbers/
执行结果

解题思路
总体思路:DFS递归遍历所有节点,递归函数增加一个形参path,用于记录根节点到当前节点这条路径上所有数字拼接成的字符串,最后把所有path转成数字并累加即可。
官解直接使用10进制计算,时长和内存都会低一些。这个解法思路算简单,时间复杂度和空间复杂度也跟官解一样,但执行时长和内存消耗略高,问题主要在以下两点:
- 时间主要消耗在:
paths.push()、字符串累加、最后多了一步paths转换累加- 内存主要消耗在:存储
paths、每个dfs调用栈的字符串形参path、末尾的paths.reduce的回调函数的调用栈空间
代码
var sumNumbers = function (root) {
const paths = [];
function dfs(node, path) {
if (!node) return;
if (!node.left && !node.right) paths.push(path + node.val);
dfs(node.left, path + node.val);
dfs(node.right, path + node.val);
}
dfs(root, '');
return paths.reduce((acc, cur) => +cur + acc, 0);
};